Tần số và chu kỳ là hai khái niệm nền tảng trong vật lý, đặc biệt là khi nghiên cứu dao động và sóng. Chúng không chỉ xuất hiện trong các bài học phổ thông mà còn đóng vai trò quan trọng trong kỹ thuật, âm học và đời sống hằng ngày. Bài viết được daigioca biên soạn nhằm giúp người học hiểu sâu và vận dụng tốt hai đại lượng này.
Tần số và chu kỳ là gì?
Trong bất kỳ chuyển động lặp lại nào như con lắc, dòng điện xoay chiều hay sóng âm thanh, hai đại lượng mô tả nhịp điệu và tốc độ là tần số và chu kỳ. Để học hiệu quả, cần phân biệt rõ hai khái niệm này.
Khái niệm tần số (f)
Tần số (ký hiệu là f) biểu thị số lần dao động xảy ra trong một giây. Nó phản ánh tốc độ của chuyển động lặp lại. Nếu một con lắc dao động 5 lần mỗi giây, ta nói nó có tần số 5 Hz.

Đơn vị của tần số là Hertz (Hz), lấy theo tên của nhà vật lý Heinrich Hertz – người đầu tiên tạo ra và phát hiện sóng điện từ. Tần số càng cao, dao động càng nhanh; ví dụ như âm thanh có tần số cao thì nghe “chói tai”, còn tần số thấp thường trầm và ấm.
Các loại tần số thường gặp
Tần số là yếu tố xác định chất lượng và tính ổn định của nhiều thiết bị điện – điều mà daigioca thường nhấn mạnh trong các tài liệu kỹ thuật. Tần số xuất hiện trong nhiều hiện tượng tự nhiên và kỹ thuật:
- Dao động cơ học: như con lắc đồng hồ, dây đàn rung…
- Dòng điện xoay chiều: tại Việt Nam là 50Hz, còn tại Mỹ là 60Hz.
- Âm thanh và sóng âm: trong âm nhạc, tần số quyết định cao độ của âm thanh.
Công thức tính tần số và chu kỳ cơ bản
Việc học vật lý sẽ hiệu quả hơn nếu người học nắm được công thức tính toán đơn giản giữa tần số và chu kỳ. Đây là hai đại lượng liên quan mật thiết với nhau theo công thức nghịch đảo.
Công thức cơ bản
Nếu biết một đại lượng, có thể tính được đại lượng còn lại. Đây là công cụ nền tảng trong các bài tập dao động điều hòa.
- f=1ThoặcT=1ff = \frac{1}{T} \quad \text{hoặc} \quad T = \frac{1}{f}f=T1hoặcT=f1.
Trong đó:
- f là tần số (Hz)
- T là chu kỳ (s)
Ví dụ minh họa
Một con lắc dao động hết 1 vòng trong 2 giây, nghĩa là chu kỳ T = 2s. Khi đó, tần số:
- f=12=0.5 Hzf = \frac{1}{2} = 0.5\, \text{Hz}f=21=0.5Hz
Nếu một vật dao động 10 lần trong 5 giây thì tần số sẽ là:
- f=105=2 Hz,T=12=0.5 sf = \frac{10}{5} = 2\, \text{Hz}, \quad T = \frac{1}{2} = 0.5\, \text{s}f=510=2Hz,T=21=0.5s

Chu kỳ là gì?
Sau khi tìm hiểu về tần số, mọi người cần thông tin để hiểu đầy đủ tần số và chu kỳ. Dưới đây là khái niệm chu kỳ và ý nghĩa của nó trong vật lý.
Khái niệm chu kỳ (T)
Chu kỳ (ký hiệu T) là thời gian để một dao động hoàn thành trọn vẹn. Đơn vị tính là giây (s). Trong thực tế, chu kỳ thể hiện độ “chậm” hay “nhanh” của một chuyển động lặp lại. Nếu một con lắc hoàn thành một vòng trong 0.2 giây thì chu kỳ của nó là 0.2s.
Ý nghĩa vật lý và ví dụ thực tiễn
Sự chính xác trong việc đo chu kỳ là nền tảng để phát triển đồng hồ, cảm biến và thiết bị đo lường hiện đại – một lĩnh vực daigioca cũng đang ứng dụng trong sản phẩm của mình. Chu kỳ giúp dự đoán khi nào chuyển động lặp lại. Các ví dụ bao gồm:
- Mặt trăng quay quanh Trái Đất có chu kỳ khoảng 27.3 ngày.
- Đồng hồ quả lắc có chu kỳ nhất định giúp đo thời gian chính xác.
- Con lắc đơn có chu kỳ phụ thuộc vào chiều dài dây và gia tốc trọng trường.
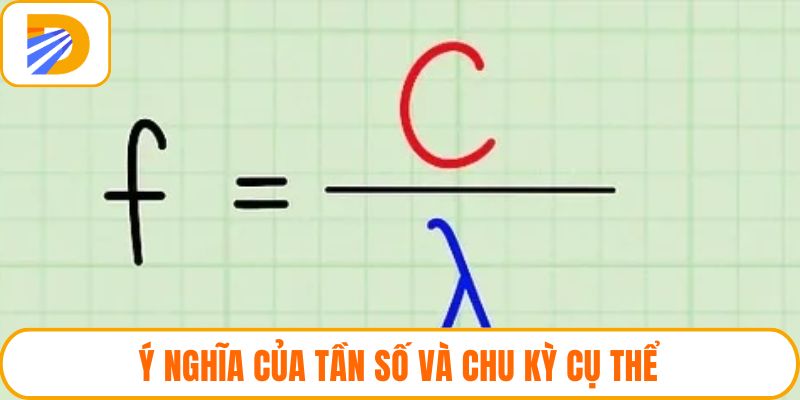
Liên hệ giữa chu kỳ và tần số
Thống kê cho thấy khi tần số tăng chu kỳ sẽ giảm và ngược lại. Mối liên hệ nghịch này rất quan trọng khi phân tích bài toán dao động.
Công thức:
- T=1fT = \frac{1}{f}T=f1
Mối liên kết giữa tần số – chu kỳ
Đây là phần trọng tâm giúp học sinh hình dung rõ cách hai đại lượng này tương tác với nhau trong thực tế và trong các bài toán. Tần số và chu kỳ là hai mặt của cùng một chuyển động lặp lại. Nếu 1 bên tăng thì bên còn lại giảm và ngược lại, điều này giúp suy luận nhanh trong các tình huống cần thiết.
Tính chất nghịch đảo tần số và chu kỳ
Đặc điểm dễ nhận thấy khi tìm hiểu tính chất nghịch đảo phải kể đến:
- Tần số cao thì chu kỳ ngắn → chuyển động nhanh.
- Tần số thấp thì chu kỳ dài → chuyển động chậm.
Ví dụ: âm thanh có tần số 440Hz (nốt La trung) có chu kỳ:
T=1440≈0.00227 sT = \frac{1}{440} \approx 0.00227\,sT=4401≈0.00227s
Ứng dụng trong giải bài tập
Khi gặp bài yêu cầu tính tần số hoặc chu kỳ, người học có thể chuyển đổi linh hoạt nhờ công thức cơ bản. Dù đề bài không cho trực tiếp f hay T, ta vẫn có thể suy luận từ số dao động và thời gian. Việc này sẽ được hướng dẫn cụ thể trong phần sau.
Hướng dẫn phân tích bài toán về tần số – chu kỳ
Phân tích chính xác bài toán là kỹ năng then chốt để giải quyết thành công các dạng dao động điều hòa. Dưới đây là hướng dẫn theo từng bước để người học có thể giải được mọi bài liên quan đến tần số và chu kỳ.
Xác định dạng bài
Việc xác định đúng dạng giúp lựa chọn công thức phù hợp. Tuy nhiên trước tiên mọi người cần đọc kỹ đề và xác định xem bài thuộc dạng:
- Dao động điều hòa cập nhật của con lắc lò xo.
- Dao động tuần hoàn của vật chuyển động tròn đều.
- Bài toán tính số lần dao động trong khoảng thời gian cố định.

Ghi lại dữ kiện và đổi đơn vị
Lưu ý khi phân tích bài toán, bạn cần ghi lại những dữ kiện cũng như tiến hành đổi đơn vị phù hợp, cụ thể:
- Thời gian có thể cho bằng phút hoặc mili giây → cần đổi về giây.
- Số dao động cần hiểu là “toàn phần” hay “một phần” để tính chính xác.
Ví dụ: “vật dao động 300 lần trong 5 phút” → thời gian = 300s, số dao động = 300.
Vận dụng công thức từng bước
Dùng công thức:
- f=Nt,T=1ff = \frac{N}{t}, \quad T = \frac{1}{f}f=tN,T=f1
Trong đó N được gọi là số dao động, còn t là thời gian được trình bày rõ ràng từng bước, tránh bỏ qua giai đoạn biến đổi.
Ví dụ minh họa
Bài toán: Một con lắc dao động 60 lần trong 30 giây. Hỏi tần số và chu kỳ cụ thể là bao nhiêu?
Lời giải:
- Số dao động N = 60.
- Thời gian t = 30s.
- Tần số: f=6030=2 Hzf = \frac{60}{30} = 2\,\text{Hz}f=3060=2Hz.
- Chu kỳ: T=12=0.5 sT = \frac{1}{2} = 0.5\,\text{s}T=21=0.5s.
Xem thêm nội dung: Bước Sóng Và Tốc Độ Truyền – Kiến Thức Nền Tảng Vật Lý
Mẹo ghi nhớ tần số và chu kỳ
Hiểu rõ bản chất, vận dụng công thức linh hoạt và phân tích bài toán đúng cách là yếu tố quyết định để học tốt. Để học tốt hai đại lượng này, có thể áp dụng một số phương pháp sau:
- Ví dụ: Một vòng xe = 1 chu kỳ. Xe quay càng nhanh (tần số tăng), thời gian hoàn thành 1 vòng càng ngắn (chu kỳ giảm).
- Vẽ sơ đồ kết nối: f ↔ T, f = N/t, T = 1/f giúp người học ghi nhớ nhanh và lâu.
- Tự đếm nhịp tim, số vòng bánh xe quay trong 10s… là cách tốt để luyện phân tích bài toán liên quan tần số và chu kỳ.
Tổng kết
Tần số và chu kỳ là hai đại lượng then chốt khi nghiên cứu các chuyển động lặp lại trong vật lý. Chúng có mối quan hệ nghịch đảo đơn giản nhưng cực kỳ hiệu quả trong phân tích. Daigioca hy vọng rằng kiến thức này sẽ hỗ trợ tích cực cho quá trình học tập và nghiên cứu.

