Tần số và chu kỳ luôn khiến nhiều người học cảm thấy choáng ngợp ngay từ những dòng đầu tiên trong đề thi. Thế nhưng, ẩn sau vẻ ngoài phức tạp đó là những quy luật logic có thể được xử lý gọn gàng nếu nắm đúng phương pháp. Bài viết dưới đây tại daigioca sẽ mở ra cách tiếp cận bài tập nhanh chóng, mạch lạc, không rối rắm.
Kiến thức cơ bản về tần số và chu kỳ
Để giải nhanh các dạng bài tập vật lý, điều quan trọng là phải hiểu rõ bản chất của tần số cùng với chu kỳ. Đây là hai khái niệm luôn xuất hiện song hành trong các chuyên đề liên quan đến dao động và sóng
Định nghĩa tần số và chu kỳ
Trong dao động điều hòa, tần số cùng với chu kỳ là hai yếu tố phản ánh tốc độ lặp lại của một chuyển động theo thời gian. Chu kỳ (T) là khoảng thời gian cần thiết để một dao động hoàn tất một vòng đầy đủ. Ngược lại, tần số (f) cho biết số lần dao động xảy ra trong một giây. Mối liên hệ giữa chúng thể hiện qua công thức: f=1T.
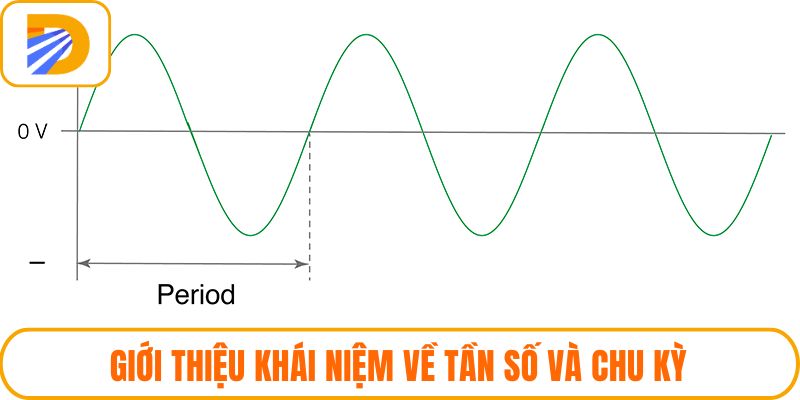
Tần số càng lớn thì dao động xảy ra càng nhanh, nghĩa là vật thực hiện nhiều vòng hơn trong một khoảng thời gian ngắn. Ngược lại, chu kỳ dài cho thấy dao động diễn ra chậm hơn, thời gian để hoàn thành một vòng chuyển động kéo dài hơn. Hai đại lượng này thường dùng trong các dạng bài tính toán tốc độ rung hoặc số lần lặp lại của chuyển động.
Đơn vị đo và cách chuyển đổi
Đơn vị đo của tần số và chu kỳ được quy định rất rõ ràng trong hệ SI. Tần số được đo bằng hertz (Hz), tức là số dao động trong một giây. Trong khi đó, chu kỳ được đo bằng giây (s), thể hiện thời gian hoàn thành một dao động. Những đơn vị này thường xuất hiện dưới dạng lũy thừa như kHz (kilohertz), ms (mili giây), hoặc µs (micro giây).
Khi giải bài tập, người học cần cẩn trọng trong bước chuyển đổi giữa các đơn vị. Ví dụ, một chu kỳ 20 mili giây phải được đổi thành 0,02 giây trước khi đưa vào công thức tính toán. Sai sót trong chuyển đổi đơn vị là nguyên nhân phổ biến khiến kết quả trở nên lệch lạc.
Tần số và chu kỳ có mối liên hệ nghịch biến, vì vậy việc dùng đúng đơn vị giúp xác định chính xác đại lượng cần tìm. Ngoài ra, thao tác chuyển đổi còn giúp tránh nhầm lẫn giữa các hệ số như 1000ms = 1s, hay 1 kHz = 1000 Hz. Việc thành thạo những phép quy đổi đơn giản này là yếu tố quyết định tốc độ xử lý bài toán trong phòng thi.
Các dạng bài tập về tần số và chu kỳ cho mọi người nắm rõ
Tần số cùng với chu kỳ thường xuyên xuất hiện trong các bài kiểm tra vật lý ở mọi cấp độ. Mỗi dạng bài đều có cách tiếp cận riêng, yêu cầu hiểu đúng khái niệm và vận dụng công thức linh hoạt.
Dạng 1 – Tính tần số khi biết chu kỳ
Tính tần số và chu kỳ là dạng bài đầu tiên giúp người học làm quen khái niệm. Khi đã biết chu kỳ T, việc xác định tần số f khá đơn giản thông qua công thức f=1T. Giá trị thu được thể hiện số lần dao động trong một giây, thường có đơn vị là hertz.
Chu kỳ càng nhỏ thì tần số càng lớn, phản ánh mức độ dao động nhanh. Ví dụ, chu kỳ là 0,02 giây sẽ cho kết quả tần số bằng 50 Hz. Đây là kiểu bài thường gặp trong các đề kiểm tra cơ bản và cũng là bước đệm cho các bài khó hơn. Khi giải, cần đổi đơn vị chu kỳ sang giây trước khi thực hiện phép chia.
Trong phần này, điều cần lưu ý là tính chính xác của số liệu đầu vào. Đảm bảo chu kỳ được nhập đúng định dạng giúp quá trình giải toán không gặp lỗi sai số, nhất là khi sử dụng đơn vị như mili giây hay micro giây.
Dạng 2 – Tính chu kỳ khi biết tần số
Khi đề bài cho biết tần số dao động, việc xác định chu kỳ sẽ ngược lại hoàn toàn. Công thức T = 1f giúp chuyển đổi nhanh từ số dao động mỗi giây sang khoảng thời gian thực hiện một chu trình đầy đủ. Đây là kỹ năng quan trọng trong các bài tập tần số và chu kỳ liên quan đến dao động cơ hoặc dòng điện xoay chiều.
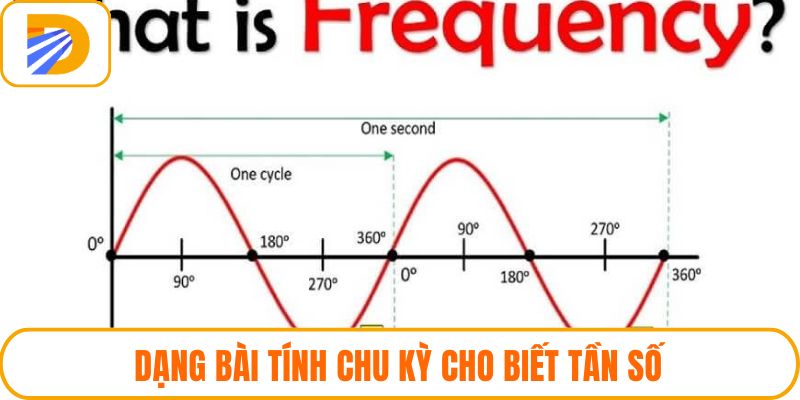
Ví dụ, nếu một vật dao động với tần số 100 Hz, chu kỳ của nó sẽ là 0,01 giây. Điều quan trọng là phải giữ đồng nhất đơn vị đo để tránh sai lệch trong kết quả cuối cùng. Tần số có thể được cho dưới dạng kilohertz, cần đổi về hertz trước khi tính chu kỳ.
Dạng 3 – Áp dụng trong dao động điều hòa
Trong dao động điều hòa, tần số và chu kỳ đóng vai trò cốt lõi trong việc mô tả đặc điểm chuyển động. Các đại lượng này giúp xác định thời gian một vật hoàn thành một vòng dao động, từ đó tính được li độ, vận tốc, hay gia tốc tại các thời điểm cụ thể.
Công thức liên quan đến tần số như ω=2f và chu kỳ như T=2 thường xuất hiện trong các bài kiểm tra học kỳ. Việc nắm vững mối liên hệ giữa chu kỳ, tần số và tần số góc giúp giải quyết nhanh chóng các phương trình dao động.
Xem thêm nội dung: Bước Sóng Và Tốc Độ Truyền – Hướng Dẫn Phân Tích Bài Toán
Mẹo giải bài tập nhanh về tần số và chu kỳ
Việc nắm rõ mẹo giải nhanh giúp tiết kiệm đáng kể thời gian trong quá trình xử lý các dạng bài này. Khi nhận diện đúng dữ kiện, kết hợp cùng hệ thống công thức đơn giản và luyện tập dạng trắc nghiệm thực tế, việc hoàn thành bài toán trở nên dễ dàng và chính xác hơn.
Xác định dữ kiện trọng tâm
Để giải nhanh bài tập liên quan đến tần số và chu kỳ, điều đầu tiên cần thực hiện là nhận diện chính xác dữ kiện chính. Một bài toán thường cung cấp nhiều thông tin, tuy nhiên không phải chi tiết nào cũng cần thiết cho quá trình tính toán. Việc xác định đúng số liệu liên quan trực tiếp đến chu kỳ hoặc tần số sẽ giúp rút ngắn thời gian xử lý.
Người học nên chú ý các thông số đặc trưng như số dao động, thời gian hoàn thành hoặc số vòng quay. Nếu đề bài đưa ra chu kỳ hoặc tần số góc, cần xác định vai trò của từng đại lượng để chọn công thức phù hợp. Mọi dữ kiện không phục vụ trực tiếp cho phép tính đều có thể được bỏ qua để tránh rối loạn tư duy.
Sử dụng bảng công thức tóm gọn
Tổng hợp công thức là công cụ không thể thiếu trong quá trình giải bài tập về tần số và chu kỳ. Thay vì nhớ máy móc, nên trình bày các công thức cơ bản theo sơ đồ tư duy hoặc bảng tóm tắt gọn gàng. Điều này giúp tăng tốc độ tra cứu và giảm thiểu sai sót trong quá trình áp dụng.
Các công thức cần thiết bao gồm: f = 1/T, T = 1/f, ω = 2πf và mối quan hệ giữa chu kỳ, tần số, vận tốc, gia tốc trong dao động điều hòa. Mỗi khi gặp bài toán cụ thể, chỉ cần chọn đúng biểu thức tương ứng, mọi phép tính trở nên rõ ràng và logic.
Luyện tập bài về tần số và chu kỳ với câu hỏi trắc nghiệm
Các câu hỏi dạng này thường có dữ liệu ngắn gọn, yêu cầu tính toán nhanh gọn và chính xác. Việc thực hành liên tục giúp não bộ ghi nhớ biểu thức, rèn luyện kỹ năng lọc dữ kiện và cải thiện tốc độ xử lý.

Nên ưu tiên các đề tổng hợp có độ khó tăng dần. Bắt đầu từ bài cơ bản, sau đó tiến đến các câu hỏi có yếu tố nhiễu nhằm tăng khả năng phán đoán. Khi quen tay, mỗi bài toán chỉ cần vài giây là có thể tìm được đáp án.
Kết luận
Tần số và chu kỳ không còn là trở ngại khi phương pháp đã được cụ thể hóa bằng các bước xử lý rõ ràng, ứng dụng được ngay. Hiểu bản chất – vận dụng đúng – phản xạ nhanh chính là ba yếu tố quyết định kết quả. Daigioca không chỉ hỗ trợ lý thuyết mà còn gợi mở kỹ thuật giải bài hiệu quả, tiết kiệm thời gian và nâng cao độ chính xác trong từng câu hỏi.

