Định luật Faraday không chỉ là một phát hiện mang tính cách mạng trong lĩnh vực vật lý, mà còn là nền tảng cho những ứng dụng công nghệ hiện đại. Được đặt theo tên của nhà bác học thiên tài Michael Faraday, định luật này gắn liền với tiến trình phát triển của khoa học điện từ. Đội ngũ daigioca tổng hợp chi tiết vai trò của định luật này trong việc định hướng giáo dục khoa học và công nghệ.
Tổng quan về định luật Faraday
Không thể nói về định luật Faraday mà không nhắc đến Michael Faraday – một trong những nhà bác học có ảnh hưởng lớn nhất mọi thời đại. Dù sinh ra trong một gia đình nghèo tại Anh, ông đã tự học và cống hiến trọn đời cho khoa học. Sự nghiệp của Faraday đánh dấu một bước ngoặt khi ông phát hiện ra hiện tượng cảm ứng điện từ – nền tảng cho định luật mang tên ông.

Hoàn cảnh ra đời của định luật gắn liền với thời kỳ bùng nổ nghiên cứu về điện từ vào thế kỷ XIX. Vào năm 1831, Faraday thực hiện các thí nghiệm cho thấy sự biến thiên từ thông qua một mạch kín có thể tạo ra dòng điện. Đây là phát hiện then chốt mở ra kỷ nguyên công nghệ điện năng.
Trong hệ thống các định luật điện từ, định luật Faraday giữ vai trò quan trọng bên cạnh các định luật của Ampère, Lenz, và Maxwell. Nó không chỉ là một biểu thức toán học mà còn là kim chỉ nam cho hàng loạt thiết bị điện tử ngày nay.
Phát biểu định luật Faraday
Để hiểu rõ hơn về định luật Faraday, chúng ta cần bắt đầu từ phát biểu gốc của nó: “Suất điện động cảm ứng trong một mạch kín tỉ lệ thuận với tốc độ biến thiên từ thông qua mạch đó.”
Hiểu đơn giản, nếu từ trường xuyên qua một mạch kín thay đổi theo thời gian, dòng điện sẽ được sinh ra trong mạch. Điều này đồng nghĩa, chỉ cần có sự thay đổi – dù nhỏ – về từ thông, sẽ xuất hiện dòng điện cảm ứng.
Các yếu tố ảnh hưởng đến suất điện động cảm ứng bao gồm cường độ từ trường, diện tích mạch kín, tốc độ biến thiên, và góc giữa mặt phẳng mạch và vectơ từ trường. Hiểu được các yếu tố này sẽ giúp người học dễ dàng ứng dụng định luật vào thực tế.
Cơ sở lý thuyết và biểu thức toán học
Trước khi áp dụng, ta cần nắm vững biểu thức tổng quát của định luật Faraday:
E=−dΦdt\mathcal{E} = – \frac{d\Phi}{dt}E=−dtdΦ
Trong đó:
- E\mathcal{E}E là suất điện động cảm ứng (đơn vị Vôn).
- Φ\PhiΦ là từ thông qua mạch kín (đơn vị Weber).
- ttt là thời gian.
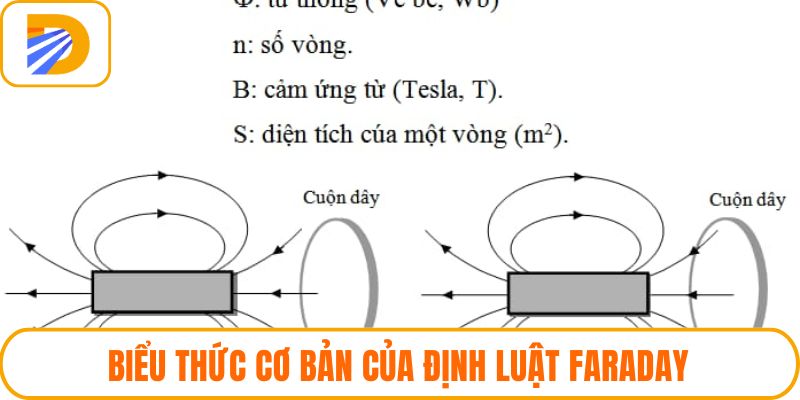
Dấu “trừ” trong công thức không phải là một chi tiết phụ. Nó thể hiện định luật Lenz, rằng dòng điện cảm ứng sinh ra có chiều chống lại nguyên nhân gây ra nó – tức là sự biến đổi từ thông.
Ứng dụng của định luật Faraday trong thực tế
Từ biểu thức đơn giản nhưng sâu sắc trên, định luật Faraday được ứng dụng rộng rãi trong cuộc sống. Hai câu dẫn sau sẽ giúp chúng ta hiểu rõ vai trò của định luật này trong các thiết bị điện tử và công nghiệp.
Máy phát điện
Một trong những minh chứng hùng hồn nhất cho định luật này là máy phát điện. Trong máy phát, một cuộn dây quay đều trong từ trường – hoặc từ trường quay quanh cuộn dây – khiến từ thông thay đổi liên tục theo thời gian, sinh ra dòng điện xoay chiều.
Nguyên lý này không thay đổi dù máy phát điện cỡ lớn trong nhà máy hay chiếc đèn pin tự phát sáng bằng tay quay. Cấu tạo gồm nam châm, cuộn dây và bộ chuyển động cơ học. Dòng điện được tạo ra một cách liên tục khi có sự biến thiên từ thông.
Biến áp (máy biến thế)
Biến áp – thiết bị giúp truyền tải điện năng hiệu quả – cũng tuân theo định luật Faraday. Khi dòng điện xoay chiều đi qua cuộn sơ cấp, từ trường biến thiên được tạo ra và truyền qua lõi sắt đến cuộn thứ cấp, tạo ra suất điện động cảm ứng.
Tỉ lệ giữa số vòng dây của hai cuộn liên hệ trực tiếp đến hiệu điện thế đầu vào và đầu ra. Đây là nguyên lý không thể thiếu trong hệ thống điện quốc gia.
Ứng dụng trong đời sống hàng ngày
Không dừng lại ở quy mô công nghiệp, định luật Faraday còn hiện diện trong nhiều thiết bị quen thuộc: đèn cảm ứng, sạc không dây, bếp từ, lò vi sóng… Tất cả đều dựa vào biến thiên từ trường để tạo ra dòng điện phục vụ mục đích sử dụng. Ngoài ra, cảm biến từ dựa trên nguyên lý này được ứng dụng rộng rãi trong an ninh công nghệ cao như cửa tự động, thẻ từ, hệ thống phát hiện kim loại…

Phân tích bài toán sử dụng định luật Faraday
Bên cạnh lý thuyết, kỹ năng vận dụng vào bài tập là chìa khóa để làm chủ định luật Faraday. Hai câu sau sẽ dẫn dắt người đọc vào thế giới bài tập phong phú và các mẹo giải hiệu quả.
Các dạng bài tập thường gặp
Nắm rõ từng dạng giúp người học dễ dàng xác định công thức phù hợp và tránh sai sót. Phần lớn các đề bài xoay quanh ba dạng chính:
- Biến thiên từ thông đều theo thời gian.
- Thay đổi diện tích mạch kín (co giãn khung dây).
- Tính suất điện động cảm ứng tức thời theo thời điểm nhất định.
Phân tích bài toán mẫu 1 – Dòng điện cảm ứng sinh ra
Đề bài: Một khung dây quay đều trong từ trường đều, hãy tính suất điện động cảm ứng tại thời điểm bất kỳ.
Cách tiếp cận:
- Xác định dữ kiện: tốc độ quay, diện tích, cường độ từ trường, góc quay.
- Áp dụng công thức E=B⋅A⋅ω⋅sin(ωt)\mathcal{E} = B \cdot A \cdot \omega \cdot \sin(\omega t)E=B⋅A⋅ω⋅sin(ωt)
- Giải từng bước: tính ω\omegaω, xác định góc quay tại thời điểm ttt, thay vào biểu thức.
Phân tích bài toán định luật Faraday – Ứng dụng thực tiễn
Đề bài: Một máy phát điện trong nhà máy thủy điện sử dụng tua-bin quay với tốc độ ổn định. Tính công suất và dòng điện tạo ra.

Giải pháp:
- Mô phỏng sự biến thiên từ thông thông qua công thức: Φ=B⋅A⋅cos(ωt)\Phi = B \cdot A \cdot \cos(\omega t)Φ=B⋅A⋅cos(ωt)
- Sử dụng E=−dΦdt=B⋅A⋅ω⋅sin(ωt)\mathcal{E} = -\frac{d\Phi}{dt} = B \cdot A \cdot \omega \cdot \sin(\omega t)E=−dtdΦ=B⋅A⋅ω⋅sin(ωt)
Liên hệ với công suất: P=E⋅IP = \mathcal{E} \cdot IP=E⋅I, từ đó tính dòng điện.
Kinh nghiệm giải bài định luật Faraday
Để giải bài tập hiệu quả, mọi người luôn vẽ hình minh họa để nắm rõ hướng từ trường và chiều quay. Hơn nữa cần phân tích đơn vị kỹ càng để tránh sai sót trong bước cuối. Ngoài ra, mọi người không bao giờ quên kiểm tra dấu của suất điện động, đặc biệt với chiều dòng điện theo Lenz.
Những sai lầm phổ biến khi áp dụng
Ngay cả người học giỏi cũng có thể mắc lỗi khi áp dụng định luật Faraday. Hai câu sau sẽ chỉ ra những điểm cần tránh để nâng cao độ chính xác trong giải bài tập.
Một số lỗi điển hình:
- Nhầm giữa dòng điện cảm ứng (I) và suất điện động cảm ứng (E\mathcal{E}E).
- Bỏ dấu trừ trong biểu thức, dẫn đến sai chiều dòng điện.
- Không để ý tới góc θ\thetaθ, dẫn đến tính sai từ thông.
- Sai đơn vị của diện tích và từ thông – dẫn tới kết quả vô lý.
Xem thêm nội dung: Công Thức Điện Trở: Tổng Hợp Cách Tính Và Mẹo Ghi Nhớ
Tầm quan trọng của định luật Faraday trong vật lý hiện đại
Định luật Faraday không chỉ còn là công cụ học tập mà đã trở thành nền tảng cho kỹ thuật điện – điện tử hiện đại. Cơ sở hạ tầng điện năng, thiết bị gia dụng, cảm biến, máy đo, sạc không dây… tất cả đều vận hành dựa trên nguyên lý cảm ứng điện từ.
Ngoài ra, định luật là một trong bốn định luật nền tảng của lý thuyết Maxwell – trụ cột của điện động lực học hiện đại, từ đó phát triển thành công nghệ truyền dẫn năng lượng không dây, cảm ứng từ và thậm chí cả pin cảm ứng từ trong y học. Cùng với sự phát triển của năng lượng tái tạo, như điện gió hay thủy điện, định luật Faraday tiếp tục khẳng định tầm ảnh hưởng mạnh mẽ.
Kết luận
Định luật Faraday là viên gạch nền trong thế giới điện từ học, mở ra hàng loạt ứng dụng thực tiễn trong kỹ thuật và đời sống. Việc hiểu và vận dụng định luật này không chỉ giúp học tốt mà còn mở lối tới công nghệ tương lai. daigioca tự hào đồng hành trong hành trình khám phá kiến thức và lan tỏa giá trị khoa học trong ứng dụng thực hành.

