Bước sóng và tốc độ truyền không còn là cụm từ khô khan khi biết cách khai thác đúng bản chất. Mỗi bài toán ẩn chứa logic chặt chẽ, đòi hỏi tư duy hệ thống và kỹ thuật xử lý chuẩn xác. Không phụ thuộc vào công thức thuộc lòng, người học cần nắm nghệ thuật phân tích – hiểu cấu trúc dữ kiện, chọn phương pháp tiếp cận hiệu quả và tìm ra hướng giải rõ ràng tại daigioca.
Tổng quan kiến thức cần nắm về bước sóng và tốc độ truyền
Để giải nhanh bài toán sóng cơ, hiểu rõ bước sóng, tốc độ truyền là điều kiện tiên quyết. Những khái niệm tưởng chừng cơ bản này lại là gốc rễ của các dạng đề quan trọng trong chương trình vật lý.
Định nghĩa và bản chất bước sóng
Bước sóng là khoảng cách giữa hai điểm tương ứng liên tiếp trên cùng một pha dao động, thường được tính bằng mét. Trong môi trường truyền sóng đều, giá trị này mô tả chiều dài của một chu kỳ dao động. Khái niệm này không tách rời khỏi thực tế mà phản ánh độ trải dài của sóng khi truyền qua vật chất.

Bước sóng và tốc độ truyền có mối liên hệ trực tiếp thông qua tần số. Khi tần số giữ nguyên, tốc độ lan truyền thay đổi thì độ dài bước sóng cũng thay đổi theo. Việc nắm rõ bản chất giúp giải thích được hiện tượng giao thoa, khúc xạ hay phản xạ trong quá trình sóng di chuyển qua các môi trường khác nhau.
Hiểu đúng tốc độ truyền sóng
Tốc độ truyền sóng thể hiện quãng đường mà sóng lan ra trong một đơn vị thời gian. Giá trị này không phụ thuộc vào nguồn dao động mà hoàn toàn do tính chất vật lý của môi trường quyết định. Ví dụ, trong không khí, âm thanh truyền chậm hơn so với chất rắn do mật độ phân tử thưa hơn.
Khi phân tích bài toán, bước sóng và tốc độ truyền không thể tách rời nhau. Nếu tần số không đổi, sự thay đổi trong môi trường dẫn đến thay đổi vận tốc kéo theo sự thay đổi chiều dài sóng. Hiểu rõ điểm này là điều kiện cần thiết để xử lý các bài toán liên quan đến giao thoa hay truyền sóng qua nhiều lớp chất liệu khác nhau.
Công thức quan trọng cần nhớ tại daigioca
Bước sóng và tốc độ truyền được kết nối thông qua công thức cơ bản: λ = v / f, trong đó λ là độ dài sóng, v là vận tốc lan truyền và f là tần số. Đây là công thức cốt lõi cần nhớ khi làm bất kỳ bài toán nào liên quan đến dao động và sóng.
Khi làm bài, cần phân tích kỹ dữ kiện để xác định đại lượng đã cho và cần tìm. Nếu tần số và vận tốc đã biết, việc tính bước sóng trở nên đơn giản. Ngược lại, trong bài toán môi trường thay đổi, công thức này hỗ trợ điều chỉnh tính toán sao cho phù hợp từng điều kiện cụ thể. Nắm vững công thức là bước đầu để làm chủ các dạng đề.
Quy trình phân tích bài toán chuẩn xác cho người học
Để xử lý hiệu quả các bài toán liên quan đến bước sóng và tốc độ truyền, cần tuân thủ một chuỗi thao tác khoa học và có hệ thống. Mỗi bước từ đọc đề, chọn biểu thức đến thế số đều quyết định độ chính xác của lời giải.
Bước 1 – Đọc kỹ đề và xác định dữ kiện
Mở đầu quá trình phân tích, việc đọc kỹ đề là bước quan trọng để nắm được bản chất vấn đề. Cần xác định rõ những đại lượng đã cho như tần số, vận tốc, thời gian hoặc khoảng cách. Mỗi dữ kiện đều mang giá trị định hướng cho cách xử lý tiếp theo.

Khi đề bài đề cập đến bước sóng và tốc độ truyền, cần khoanh vùng ngay các thông tin liên quan đến dao động và truyền sóng. Việc hiểu đúng từng yếu tố giúp tránh nhầm lẫn trong suy luận và giảm thiểu sai số khi áp dụng công thức. Đây là bước định vị trọng tâm vấn đề.
Bước 2 – Chọn công thức bước sóng và tốc độ truyền phù hợp
Sau khi xác định dữ liệu, việc tiếp theo là tìm ra công thức đúng. Trong các bài toán về dao động sóng, công thức λ = v / f là biểu thức phổ biến, kết nối trực tiếp giữa bước sóng và tốc độ truyền thông qua tần số. Tùy theo dữ kiện, người học sẽ sử dụng biến đổi tương ứng từ biểu thức gốc.
Chọn đúng công thức sẽ giúp tiết kiệm thời gian, đồng thời giữ cho tiến trình giải bài trở nên mạch lạc. Không nên sử dụng các biểu thức phức tạp nếu dữ liệu đã đủ để áp dụng công thức đơn giản. Tập trung vào mối liên hệ giữa đại lượng là chìa khóa trong bước này.
Bước 3 – Thay số và biến đổi biểu thức
Khi đã xác định đúng công thức, tiến hành thay số là thao tác đòi hỏi sự cẩn trọng. Cần đảm bảo đơn vị thống nhất trước khi tính toán để tránh sai lệch kết quả. Ví dụ, nếu tốc độ truyền đang ở đơn vị m/s thì bước sóng cũng nên được tính bằng mét.

Giai đoạn này không chỉ là phép thế số đơn thuần mà còn yêu cầu xử lý biểu thức sao cho kết quả cuối cùng rõ ràng, có ý nghĩa vật lý. Đừng quên đối chiếu giá trị thu được với tính hợp lý của đề bài. Đây là bước hoàn thiện toàn bộ quá trình phân tích một cách chỉn chu.
Xem thêm nội dung: Công Thức Dao Động Điều Hòa Với Các Bước Giải Bài Tập Nhanh
Các dạng bài tập về công thức thường gặp trong đề thi
Việc làm chủ các dạng toán liên quan đến bước sóng và tốc độ truyền giúp nâng cao độ chính xác khi giải đề. Mỗi dạng đều có đặc điểm riêng, đòi hỏi sự hiểu thấu đáo về công thức, điều kiện môi trường và mối liên hệ giữa các đại lượng.
Tìm bước sóng khi biết vận tốc và tần số
Trong các bài toán yêu cầu xác định bước sóng, điều kiện thường là đã biết tốc độ truyền sóng và tần số dao động. Khi đó, công thức cơ bản λ = v / f được áp dụng để rút gọn quá trình giải. Cần chú ý đơn vị giữa các đại lượng phải đồng bộ để đảm bảo kết quả có giá trị thực tế.
Vận dụng linh hoạt công thức bước sóng và tốc độ truyền này đòi hỏi phải hiểu rõ bản chất dao động và truyền sóng. Nhiều bài nâng cao sẽ có thêm yếu tố nhiễu như môi trường thay đổi, đòi hỏi xử lý cẩn trọng từng bước. Xác định mối quan hệ giữa dữ kiện đầu vào sẽ giúp việc tính bước sóng trở nên nhanh chóng và chính xác.
Tính tốc độ truyền trong môi trường đặc biệt
Khi bài toán yêu cầu tìm bước sóng và tốc độ truyền, dữ liệu thường gồm bước sóng và tần số hoặc thời gian truyền qua một khoảng xác định. Việc áp dụng công thức v = λ × f là lựa chọn tối ưu, song trong môi trường không đồng nhất, cần điều chỉnh cách xử lý tùy theo tính chất vật lý.
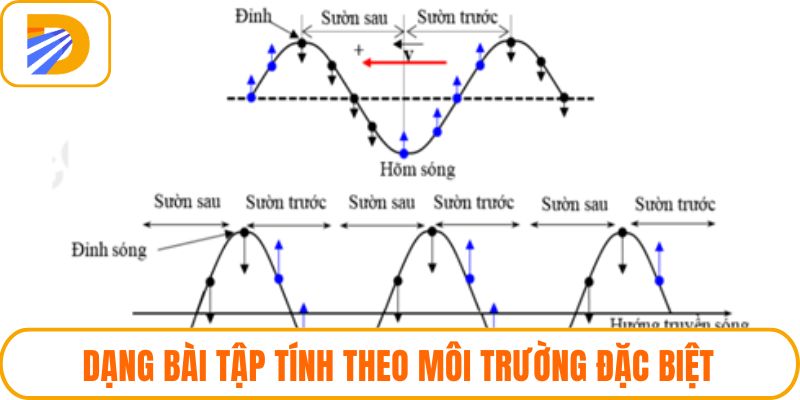
Đặc biệt trong môi trường như chất rắn, chất lỏng hoặc khí nén, tốc độ truyền có thể biến thiên. Người giải cần chú ý các yếu tố ảnh hưởng như mật độ, độ đàn hồi hoặc nhiễu loạn sóng. Nắm chắc vai trò từng tham số sẽ giúp kết quả không sai lệch trong trường hợp dữ liệu phức tạp.
Xác định tần số khi biết bước sóng và tốc độ khi làm bài toán
Bài toán yêu cầu tìm tần số thường xuất hiện trong phần ứng dụng sóng cơ học hoặc âm thanh. Khi bước sóng và tốc độ truyền được cung cấp, chỉ cần áp dụng công thức f = v / λ để tính. Dạng bài này tuy cơ bản nhưng lại dễ sai sót nếu không để ý đơn vị đo.
Việc nhận biết đúng tần số không dừng lại ở phép tính mà còn liên quan đến phân tích bản chất dao động. Trong thực tế, nhiều đề thi còn gài thêm yếu tố nhiễu hoặc thay đổi môi trường truyền, buộc người học phải cân nhắc kỹ điều kiện. Giải đúng yêu cầu sự thấu hiểu và thao tác nhanh nhạy.
Kết luận
Bước sóng và tốc độ truyền không dừng lại ở các công thức vật lý thông thường mà mở ra góc nhìn khoa học sâu sắc về quá trình truyền thông tin và năng lượng. Khi hiểu đúng cách vận dụng tại daigioca, người học không những giải bài chính xác mà còn rèn tư duy phân tích nhanh, linh hoạt.

